Аннотация

За последние две тысячи лет человечеству удалось продвинуться от понимания числовых закономерностей гармонии до числовых отношений, характеризующих жизнь. Новые знания могут стать основой широко обсуждаемых сегодня проектов искусственного интеллекта и цифровой экономики, поскольку создать их без численного описания смысла невозможно.

Введение

Сколько чисел нужно знать современному человеку, у которого есть компьютер, интернет и кредитная карточка?

Может быть столько же, сколько и древнему, который знал лишь один, два, много и куча?

Дело в том, что новые числа появляются с расширением опыта и исчезают с его оскудением. Например, представление о том, что «много» — это большая система — появилось у Пуанкаре в конце XIX века, но лишь 100 лет спустя после этого Кузьмин и Жирмунский раскрыли его устойчивое числовое содержание. Тем не менее, еще в YI веке до нашей эры на одном из устойчивых чисел, равном 7, Пифагор основал доктрину Гармонии и Музыки Сфер. Через 1700 лет Фибоначчи на примере роста популяции кроликов открыл числовую последовательность, характеризующую жизнь. А спустя 800 лет после этого Колмогоров установил закон распада больших систем различной природы. Через 50 лет после этого автору удалось его расширить на случай неустойчивой самоорганизации систем. В результате за 2,5 тысячи лет человечеству удалось продвинуться от понимания гармонии до числовых отношений, характеризующих жизнь. Эти новые знания могут лечь в основу широко обсуждаемых сегодня проектов искусственного интеллекта и цифровой экономики, поскольку без численного описания их смысла не обойтись.

Один, два, много и куча

У индейцев Южной Америки, сохранивших первобытный образ жизни, есть всего 4 понятия, связанных со счетом. Один, два, много и куча. Детальный смысл их представлений нам не известен, но понятно, что чрезвычайно малое количество показателей счета может свидетельствовать не только об их количественном значении, но качественном содержании.

Что такое 1, понятно – это целое.

Что значит 2, тоже. Двойственность и начало множества.

А что значит много?

Много – это «большая система» Пуанкаре

Удивительное дело, но почему числа три, четыре и т.д. можно заменить одним словом «много», современный человек понял лишь в конце XIX века. Произошло это благодаря изысканиям математика, физика и философа Пуанкаре, который доказал, что системы, состоящие более чем из двух частиц, говоря математическим языком, не интегрируемы. Т.е. их совокупное поведение не может быть сведено к совокупности поведения отдельных частиц. Он даже высказал гипотезу почему. Потому, что между частицами возможно резонансное взаимодействие. Такие временно устойчивые системы, обладающие непредсказуемым поведением, он предложил называть «большими». С первой такой непредсказуемой системой из трех частиц ученые столкнулись в середине XX века, когда не смогли точно проложить траекторию полета ракеты с Земли на Луну. В результате первые исследовательские аппараты вынуждены были запускаться в сторону Луны.

В жизни же людей непредсказуемый характер поведения временно устойчивой системы их трех человек хорошо известен под названием любовный треугольник.

Через 100 лет после Пуанкаре благодаря трудам российских ученых Кузьмина и Жирмунского выяснилось, что временно устойчивый характер имеют не все системы, а лишь те, численность которых достигает критических уровней развития, подчиняющихся экспоненциальной зависимости по основанию натурального логарифма е2,72.

Перечислим первые из них, округлив значения до целого числа:

1. N = 3, 7, 15, 20, 54, 90…

И приведем наиболее известные устойчивые социальные системы такой размерности. Международные структуры G7 и G20, 15 республик СССР, 51 губерния Российской империи Екатерины II, 55 штатов и островных территорий современных США, 89 субъектов современной Российской Федерации.

Таким образом, мы можем заключить, что если вы сталкиваетесь с системами приведенного выше ряда чисел, то высока вероятность того, что они являются устойчивыми.

Первым, кто задумался о качественном смысле чисел из этой серии, был Пифагор.

Число 7, в частности, легло в основу пифагорейской Музыки Сфер.

Пифагорейство
или Музыка сфер

Приблизительно за 500 лет до нашей эры в опытах со струнами Пифагор обнаружил ряды гармонических чисел, соотношения которых описывают музыкальный ряд. Его опыты показали, что когда струна при определенном весе гири издавала звук, то для повышения этого звука на октаву, требовался вдвое больший вес гири; для квинты — только на треть больший, для кварты — на четверть, для тона — на одну восьмую, для полутона — на одну восемнадцатую, или около этого. То же самое происходит, когда струна сжимается посередине, она дает октаву от первоначального звука; на одной трети длины — квинту, на четверти — кварту, на восьмой доле длины — тон, на восемнадцатой — полутон.

Т. о. Пифагор опытным путем установил количественную взаимосвязь частот колебаний струны (f) с ее линейными размерами (l)

2. f ~ 1/l

или периодов колебаний (Т) с длиной струны (l)

Т ~ l ,

Одновременно с этим он определил числовые соотношения длин струн для консонанса (слияние тонов),

3. l1/l2 = 1/2, 2/3, 3/4.

При этом интервал оказывался тем звучнее, чем меньше число п=1,2,3…

Полагая, далее, что всякое движение сопровождается излучением волн, он посчитал, что вследствие этого должна существовать и не слышанная человеческим ухом музыка движения небесных тел Солнечной системы. Некая Музыка Сфер, под которую движется, постоянно видоизменяясь, вся наша жизнь.

В дальнейшем на основе этой гипотезы сложились многовековые традиции сакральной нумерологии, согласно которой события и явления как личной, так и общественной жизни обязаны согласовываться с числами.

Например, ум, так как он постоянен, тождествен себе и «начальствен» – это единица. Помимо этого единица соответствует мужскому началу, а двойка — женскому. Потому, что женщина раздваивается при родах. Вследствие этого, двойка одновременно – это еще начало и символ множественности и неопределенной бесконечности (т.е. неустойчивости). Мужчина в ряду пифагорейских представлений – это три – символ определенности (устойчивости). Поэтому брак как соединение мужчины и женщины – это пять, (2+3=5) . А первое «квадратное» число четыре означает справедливость, потому, что ее отличительное свойство, ярко проявляющееся в квадрате, состоит в равенстве, или эквивалентности сторон. Правда, одни пифагорейцы считали справедливостью четыре (первое чётное квадратное), а другие – девять (первое квадратное нечётное). «Подходящий момент» — это семь, так как самые важные моменты в жизни человека происходят по седьмицам: младенец полностью формируется в семь месяцев (210 дней), зубы появляются через семь месяцев после рождения, половая зрелость наступает через две седьмицы (14 лет), а борода вырастает через три (в 21 год). На этом числе семь Пифагор и основал свою доктрину Гармонии и Музыки Сфер, назвав «тоном» расстояние от Луны до Земли.

Возникшая в результате трудов Пифагора философия числа легла не только в основу сакральной нумерологии, но и всей математической физики.

Первыми учеными в ряду последователей Пифагора стали физики Галилей и Кеплер, сформулировавшие законы движения материальных тел в виде кратких числовых отношений – математических формул. И все последующее развитие физики явилось, по сути, неким новым прочтением пифагорейства, в рамках которого законы природы оказались всего лишь отношениями чисел. «В том-то и вся беда с физикой — писал по этому поводу Р. Фейнман — что она должна быть математической»

А может быть это и не беда физики, а дальнейшее поле ее деятельности, разбираться вслед за Пифагором со смыслом все новых и новых чисел, рождающихся в жизни человечества?

Какой смысл, например, человек вкладывает в понятие куча?

Куча
или о чем не знал Пифагор

Консонанс, созвучие, гармония далеко не единственная форма поведения больших систем. Во многих случаях в них может возникать и диссонанс, и белый шум. Однако об этих и других особенностях поведения больших систем задумались лишь тысячелетия спустя после Пифагора.

Так, в опытах геофизиков, самым известным из которых является Рихтер (шкала землетрясений Рихтера), выяснилось, что куча является своеобразной физической системой, поведение которой моделирует переходное состояние между порядком (песочной пирамидой) и хаосом землетрясений. Т.е. куча, по сути, обозначает множество явлений, названных в середине XX веке физиком Хакеном словом синергетика.

Детальное исследование числовых рядов поведения кучи песка показало, что оно подобно поведению потоков воды, теоретическое объяснение которого в 1941 году предложил Колмогоров. Согласно его гипотезе период колебаний сплошной среды (Т) пропорционален ее размерам (l) в степени 2/3

4. Т ~ l^2/3

Сравнивая эту закономерность с уравнением Пифагора (2), следует заметить, что динамическое поведение кучи отличается от поведения струн лишь степенью зависимости.

На качественном же уровне уравнение Колмогорова говорит, что чем больше пространственные размеры потрясений среды, тем реже они встречаются (больше период между ними).

Графический характер этой закономерности показан на рис. 1.

Бывает хуже, но реже

Эта качественная интерпретация закона Колмогорова, описывает уже не столько поведение кучи песка или потоков воды, сколько коллизии нашей жизни. Действительно, чем чаще они встречаются, тем меньше их значение.

Закон Колмогорова, однако, не говорит о характере самой последовательности критических событий жизни во времени или в пространстве. Этот феномен в виде роста численности популяции кроликов со временем или порядка расположения листьев на ветке исследовал более 800 лет назад Леонардо Пизанский, больше известный как Фибоначчи. В 1202 году (приблизительно 1700 лет спустя после Пифагора) в «Книге абака» он описал этот процесс последовательностью чисел

5. N = 1, 1, 2, 3, 5, 8, 13, 21, 34, …

В асимптотике отношение двух чисел ряда Фибоначчи приводит к «золотому сечению», которое благодаря трудам Леонардо да Винчи приобрело со временем характер принципа художественного совершенства.

Последовательность чисел Фибоначчи (5) вместе с уравнением Колмогорова (4) можно было бы считать некоей музыкой жизни, как законы Пифагора (2) и (3) Музыкой Сфер, если бы была точно также установлена взаимосвязь физических размеров живых систем с частотой (периодом) колебания их состояния.

Как ни странно, но сам этот вопрос о связи размеров живых систем с длительностью их жизни впервые был поставлен физиологом Пироговым лишь через 650 лет после Фибоначчи — в середине XIX века.

Ответить же на него удалось еще спустя более 150 лет — в начале XXI века. Этот ответ демонстрирует график 1, построенный Серебровым и автором в 2001 году. [1].

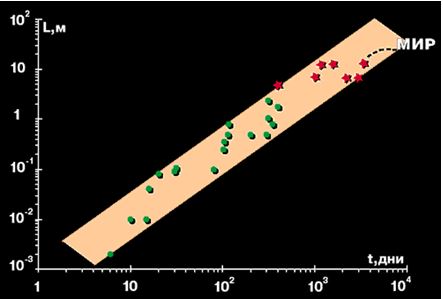
Рис. 1. Зависимость максимальных линейных размеров эмбрионов (кружки) и космических аппаратов (звездочки) от времени их жизни (штриховая линия — траектория роста станции «Мир», полоса — закон Колмогорова).
Точками на рисунке показаны масштабы времени и пространства, характеризующие эмбриональный период развития наиболее известных животных нашей планеты, а звездочками – данные о размерах советских космических аппаратов и интервалах времени от начала их проектирования до окончания жизни в космосе. На графике хорошо видно, что космические аппараты как бы продолжили эстафету биологической жизни на Земле. Поскольку характеризующая их числовая закономерность оказались неотличима от закономерности роста биологических систем.

Красота – это формула жизни

Сегодня представления Достоевского, Чехова или Гейне о красоте как своеобразной художественной формуле жизни (вспомним: «красота спасет мир», «в человеке все должно быть прекрасно…», «Единственная красота, которую я знаю, это здоровье»), можно дополнить результатами математических изысканий последнего времени. Как оказалось, они позволяют говорить о красоте и как о математически точном образе жизни.

К поиску формулы красоты человечество двигалось довольно долго. Так, со времен витрувимского человека Леонардо да Винчи известно, что пропорции человеческого тела соответствуют не гармоническим отношениям Пифагора 1/2, 2/3, 3/4, а золотому сечению, к которому в пределе стремится ряд Фибоначчи.

А в последнее время выяснилось, что не только золотое сечение определяет красоту, но и некая отличительная совокупность пространственных и временных пропорций всего явления в целом.

Ее удалось обнаружить благодаря теоретическому описанию динамики всплеска морской волны формулой [2].

6. Т ~ l^2/3/(1- l/L),

в которой L характеризует максимальный пространственный размер явления или системы, согласно соотношениям Кузьмина-Жирмунского.

При сопоставлении теоретической модели морской волны с эталоном ее художественного образа — «Большой волны в Канагаве» (рис. 2), японского художника середины XIX века К. Хокусая, выяснилось, что под красотой нами понимается невероятно контрастное сопряжение расцвета с угасанием, или потрясений с гармонией, или порядка с хаосом.

Как об этом писал, например, Есенин:

…будь же ты вовек благословенно,
что пришло процвесть и умереть.

Или, как показывает картина К. Хокусая, в которой плавное нарастание волны до гребня приводит к ее феерическому распаду.

Такая неожиданная трансформация упорядоченности в хаос возникает, как показывает математическая модель (6), только либо в ограниченном пространстве развития системы, либо в ограниченных интервалах времени ее жизни. В формуле (6) (в отличие от формулы (4)) это обстоятельство отражается параметром L.

Рис. 2. «Большая волна в Канагаве» художника К. Хокусая в сравнении с теоретической моделью энергии турбулентной волны автора (кривая линия)

А все живые процессы и явления на Земле ограничены. И в пространстве и во времени. Например, размерами планеты или материков, водоразделов, горных гряд и т.д. Самые крупные из этих пространственных ограничений порождают в обществе глобальные 140-летние волны экспансии, новых промышленных технологий или социальных потрясений [3]. Их наиболее яркими проявлениями в мировой истории являются: волна капитализма от Великой французской революции 1789 года до великой депрессии 1929 года и волна социализма от «Манифеста компартии» 1848 года до распада системы социализма в 1989 году.

Этот 140-летний период колебаний жизни на Земле имеет множество обертонов и гармоник, самые известные из которых составляют:

7. Т = 560, 280, 70, 35, 17-18 и 11-12, 7 и 5 лет.

Согласно принципу эргодичности Больцмана, в соответствии с которым периодам жизни системы можно поставить в соответствие размеры пространственных волн (L ~ T), частот колебаний (f = 1|T) или численности систем (n = f), отношения чисел, аналогичные временным рядам, мы можем обнаружить и в пространственной периодичности систем и численности их элементов.

Таким образом, оказывается совершенно естественным обнаружение числовых рядов красоты, жизни и гармонии как в биологической жизни на Земле, так и ее различных социальных, экономических и технических проявлениях.

Заключение

Знание является таковым, поскольку является числовым, заметил в XX веке математик Колмогоров. В XXI веке, после более полного раскрытия феномена турбулентности, можно добавить, потому, что все процессы природы ритмичны, что наилучшим и наикратчайшим образом выражается числом. Перечислим поэтому некоторые единые числовые закономерности, характеризующие поведение больших систем различной природы.

1. Гармоничное поведение (YI век до н.э.)

1/2, 2/3, 3/4,

T~ 1/l .

2. Турбулентность и самоорганизация (XX век)

3, 7, 15, 20, 54, 90…

T~ 1/l^2/3

3. Жизнь и красота (XII и XXI века)

2/3, 3/5, 5/8, 8/13, 13/21…. золотое сечение,

560, 280, 140, 70, 35, 17-18 и 11-12, 7, 5.

В середине XX века установленные к тому времени числовые закономерности природы стимулировали бурное развитие вычислительной техники. По некоторым оценкам, сегодня ее возможности вплотную приблизились к созданию искусственного интеллекта.

На наш взгляд, однако, знаний XX века для достижения этой цели не достаточно, поскольку прежде на числовом языке необходимо объяснить ЭВМ, что такое интеллект. Сделать же это возможно лишь с помощью новых математических знаний XXI века о красоте, жизни и турбулентности.
_______________________________________

Литература

3. Доброчеев О.В. Глобальные волны технологических нововведений// Космонавтика XXI века. Под ред. Акад. Чертога Б.Е. М.::СОФТ. 2010